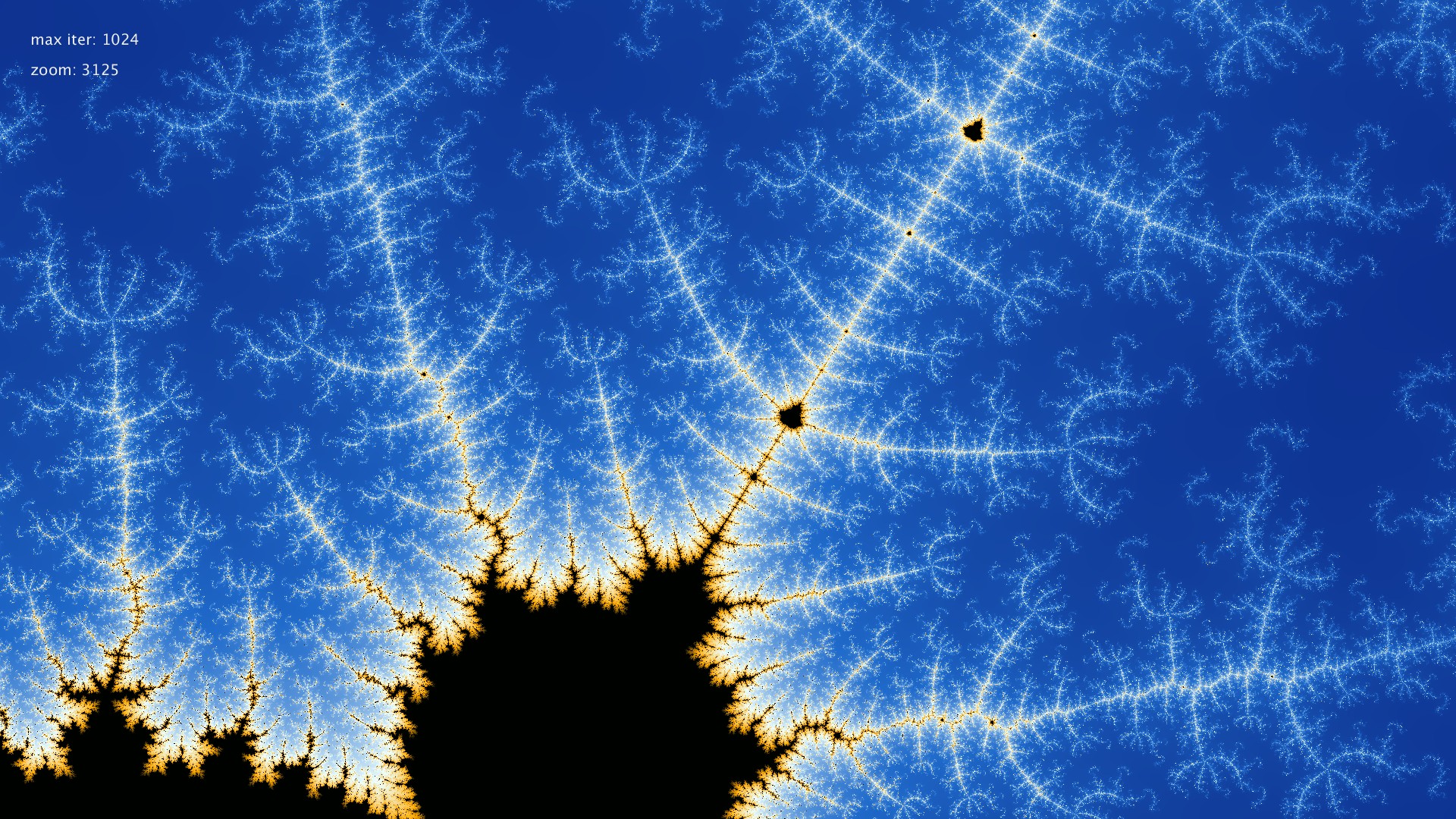
Create Your Own Meldelbrot Checker

Mendelbrot set is the subset of complex numbers. Let “c” be an arbitary complex number, and define the function: \(f_c(z) = z^2 + c\), where \(z\) start from \(0 + 0i\).

Then, for the complex number “c”, if \(f_c(z)\) won’t diverge (or go to infinity) after applying the function for infinite times, then this complex number “c” is in Mandelbrot Set.

Although the definition is pretty simple, it creates a fractal, which would give you unlimited details as long as you keep zooming in.

Before Coding

Still, there is a problem: how can we determine whether a certain point would diverge? Clearly computers cannot do calculations infinitely for infinite points, but we can apply these two strategies:

1. Indeed, we cannot apply \(f_c(z)\) for infinite times. Therefore, we set the max iteration count for the program. The larger maxIter is, the more precise the graph would be. We can adjust based on our needs.
2. We can prove that any points with absolute value greater than two (\(\sqrt{a^2 + b^2} > 2\)) will ultimately diverge. Here is the proof by induction from stackExchange:

Code Implementation with Video

Also, here is the full version of the code, and you can also check more related content in corresponding github repo:

int maxIter = 128;
double minRe = -2.5, maxRe = 1;
double minIm = -1, maxIm = 1;
boolean pressedLeft = false;
boolean pressedRight = false;
double zoom = 1.0;

color[] colors;

public void setup() {
  fullScreen();
  colors = new color[]{
    color(0, 7, 100), color(32, 107, 203), 
    color(237, 255, 255), color(255, 170, 0), 
    color(0, 2, 0)};
  //colors = new color[]{
  //  color(0), color(213, 67, 31), 
  //  color(251, 255, 121), color(62, 223, 89), 
  //  color(43, 30, 218), color(0, 255, 247)};
}

public void draw() {
  if (mousePressed && mouseButton == LEFT && !pressedLeft) {
    pressedLeft = true;
    zoomX(5);
    zoom *= 5;
  } else if (mousePressed && mouseButton == RIGHT && !pressedRight) {
    pressedRight = true;
    zoomX(1.0 / 5);
    zoom /= 5.0;
  }

  loadPixels();
  for (int y = 0; y < height; y++) {
    for (int x = 0; x < width; x++) {
      double cr = minRe + (maxRe - minRe) * x / width;
      double ci = minIm + (maxIm - minIm) * y / height;
      double re = 0, im = 0;
      int iter;
      for (iter = 0; iter < maxIter; iter++) {
        double tr = re * re - im * im + cr;
        im = 2 * re * im + ci;
        re = tr;
        if (re * re + im * im > 2 * 2) break;
      }

      int maxColor = colors.length - 1;
      //if (iter == maxIter) iter = 0;
      double mu = 1.0 * iter / maxIter;
      mu *= maxColor;
      int iMu = (int)mu;
      color color1 = colors[iMu];
      color color2 = colors[min(iMu + 1, maxColor)];
      color c = linearInterpolation(color1, color2, mu - iMu);
      pixels[x + y * width] = c;
    }
  }
  updatePixels();
  textSize(20);
  String msg1 = "max iter: " + maxIter;
  String msg2 = "zoom: " + zoom;
  fill(238);
  text(msg1, 40, 40, 280, 40);
  text(msg2, 40, 80, 280, 80);
  //println();
  //print(red(pixels[mouseX + mouseY * width]) + " ");
  //print(green(pixels[mouseX + mouseY * width]) + " ");
  //print(blue(pixels[mouseX + mouseY * width]) + " ");
}

public color linearInterpolation(color c1, color c2, double a) {
  //println(a);
  double newR = red(c1) + a * (red(c2) - red(c1));
  double newG = green(c1) + a * (green(c2) - green(c1));
  double newB = blue(c1) + a * (blue(c2) - blue(c1));
  return color((float)newR, (float)newG, (float)newB);
}

public void mouseWheel(MouseEvent event) {
  if (event.getCount() > 0) maxIter /= 2;
  if (event.getCount() < 0) maxIter *= 2;
  maxIter = constrain(maxIter, 1, 2048);
}

public void mouseReleased() {
  if (pressedLeft) {
    pressedLeft = false;
  } else if (pressedRight) {
    pressedRight = false;
  }
}

public void keyPressed() {
  double w = (maxRe - minRe) * 0.3;
  double h = (maxIm - minIm) * 0.3;
  if (keyCode == LEFT) {
    minRe -= w; 
    maxRe -= w;
  } else if (keyCode == RIGHT) {
    minRe += w; 
    maxRe += w;
  } else if (keyCode == UP) {
    minIm -= h; 
    maxIm -= h;
  } else if (keyCode == DOWN) {
    minIm += h; 
    maxIm += h;
  } else if (key == ' ') {
    saveFrame("screen-#####.jpg");
  }
}

public void zoomX(double z) {
  // set new center point at mouse point
  double cr = minRe + (maxRe - minRe) * mouseX / width;
  double ci = minIm + (maxIm - minIm) * mouseY / height;
  // zoom
  double tminr = cr - (maxRe - minRe) / 2 / z;
  maxRe = cr + (maxRe - minRe) / 2 / z;
  minRe = tminr;

  double tmini = ci - (maxIm - minIm) / 2 / z;
  maxIm = ci + (maxIm - minIm) / 2 / z;
  minIm = tmini;
}