Maze Generation and Pathfinding Algorithms
Initially, I watched coding train’s A* pathfinding algorithm and decided to make my own version. However, when finishing A*, I was thinking of generating maze first and then use A* to solve it. After that, inspired by this webpage, I thought it would be interesting to add more pathfinding algorithms like DFS, BFS, Dijkstra, and Best First.
Finally, here is what I’ll present in this post: how to make a comprehensive program that can accomplish all these requirements, which includes two Maze-Generation methods and five Pathfinding Algorithms.
Here is the Video illustration with full detail in following parts. You can also check detailed code and text explainations in remaining parts!
Maze Generation Method1 -Randomized Depth-First Search (0:06 - 0:15)
Let the random walker start fromtop-left corner and remove walls that block its route. If the walker meets dead-end, it would back-trace till getting the cell that has avaliable path.
The algorithm reapeats such process till all the cells in the maze are visited.
The algorithm’s time complexity would grow exponentially with the increase of maze size. Still, it can generate mazes with certain complexity. If you want to reduce time complexity, you can apply mathods like recursion method.
void generateMaze() {
for (Cell c : grid) {
c.show(color(20, 100));
}
for (int n = 0; n < 20; n++) {
current.visited = true;
current.highlight();
Cell next = current.checkNeighbours();
if (next != null) {
next.visited = true;
stack.add(current);
removeWalls(current, next);
current = next;
} else if (stack.size() > 0) {
current = stack.remove(stack.size() - 1);
}
if (frameCount > 10 && stack.size() == 0) {
drawFinish = true;
for (Cell c : grid) {
c.addNeighbours();
c.visited = false;
}
start.visited = true;
return;
}
}
}Maze Generation Method 2 - Purely Random Generation (3:23 - 3:29)
Loop over all cells and give a 45% chance to remove either wall around. When all cells are visited, the maze generation completes.
The biggest problem for this method is that it can’t guarantee a path between start and end. Still, we can avoid this case by regeneration and certain detection algorithm.
void generateRandom() {
removeWalls(grid[0], grid[1]);
removeWalls(grid[grid.length - 1], grid[grid.length - 2]);
for (int n = 0; n < 10; n++) {
Cell current = grid[frameCount * 10 - 10 + n];
int i = current.i, j = current.j;
ArrayList<Cell> around = new ArrayList<Cell>();
int top = current.index(i, j - 1);
int right = current.index(i + 1, j);
int bottom = current.index(i, j + 1);
int left = current.index(i - 1, j);
if (top != -1)
around.add(grid[top]);
if (right != -1)
around.add(grid[right]);
if (bottom != -1)
around.add(grid[bottom]);
if (left != -1)
around.add(grid[left]);
for (Cell neighbour : around) {
float r = random(1);
if (r < 0.4) {
removeWalls(current, neighbour);
}
}
}
for (Cell c : grid) {
c.show(color(20, 100));
}
if (frameCount > grid.length / 10 - 1) {
drawFinish = true;
for (Cell c : grid) {
c.addNeighbours();
c.visited = false;
}
start.visited = true;
}
}Pathfinding Algorithm 1 - A* (0:15 - 0:54 & 3:29 - 4:36)
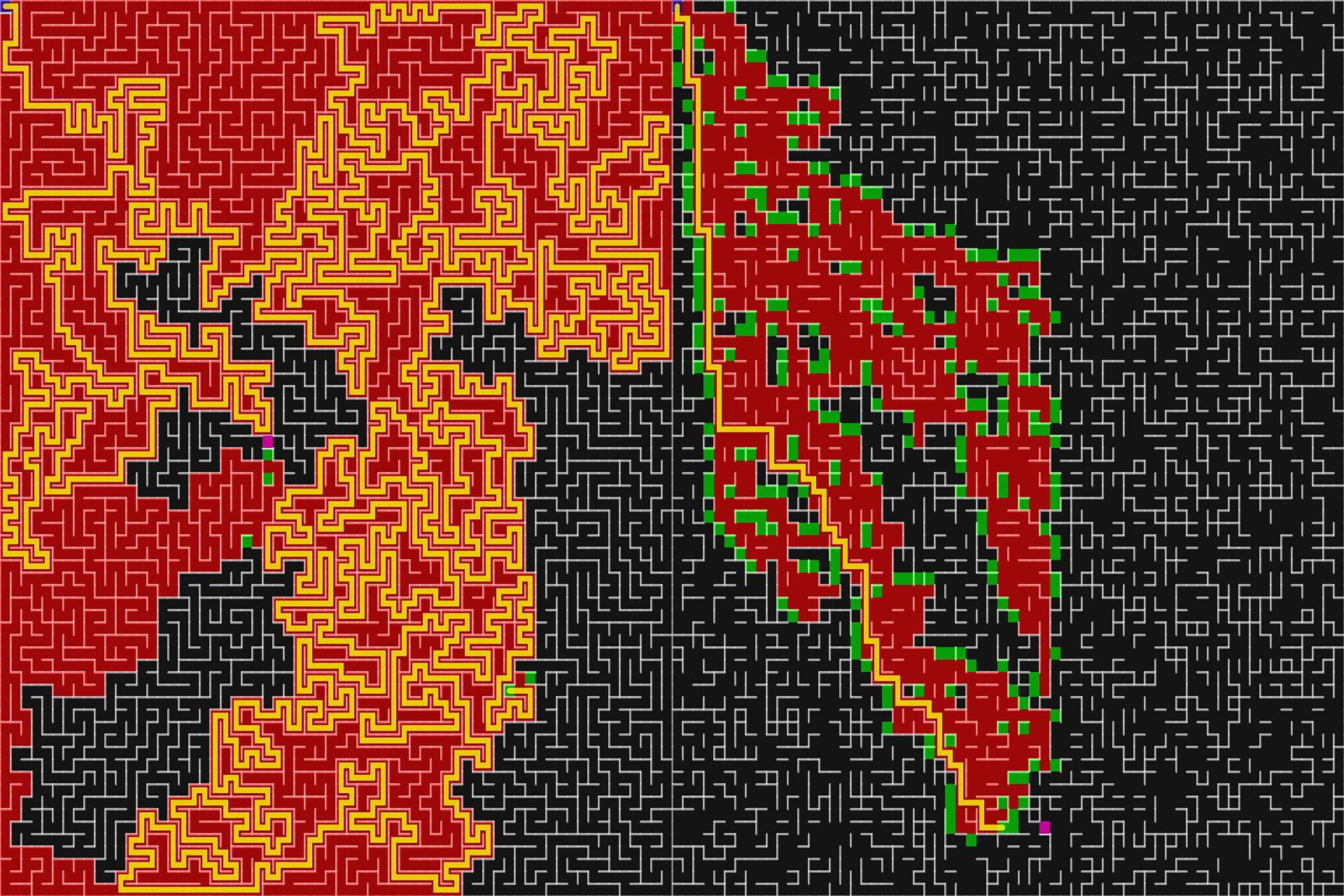
A* selects path by two factors, current route length (g value) and next cell’s length to end (h value) . Each time it choose the cell that has smallest sum of two values and push all following paths into choice stack. The algorithm repeats such process till current block is the exit.
Then, with pre-recorded route info, program backtrack from exit and print the best route
Solely view from performance, A* algorithm outperform most basic algorithms.
Also, “h” means heuristic here, which is a inspiring indicator. As we can only move towards four straight directions, I set the function that calculate the length to exit as the function that calculate the Manhattan distance.
When each cell’s h value is less than acutal best distance, A* will always find the best route. The closer h value diff from real value from lower side, the high its efficiency would be. Otherwise, taking other h-calculation method cannot guarantee finding the best path, but it can greatly increase A* efficiency.
Therefore, we can choose h function based on actual need.
Also, A* need the exact postion of the destination, or we cannot apply A*.
void AStar() {
if (route.size() > 0) {
int winner = 0;
for (int i = 0; i < route.size(); i++) {
if (route.get(i).f < route.get(winner).f ||
(route.get(i).f == route.get(winner).f && route.get(i).heuristic < route.get(i).heuristic)) {
winner = i;
}
}
current = route.get(winner);
if (current == end) {
findPath = true;
drawWindowAStar();
return;
}
route.remove(current);
closed.add(current);
ArrayList<Cell> neighbours = current.neighbours;
for (Cell neighbour : neighbours) {
if (!closed.contains(neighbour)) {
float tempG = current.g + 1;
boolean newPath = false;
if (route.contains(neighbour)) {
if (tempG < neighbour.g) {
neighbour.g = tempG;
newPath = true;
}
} else {
neighbour.g = tempG;
neighbour.visited = true;
newPath = true;
route.add(neighbour);
}
if (newPath) {
neighbour.heuristic = heuristic(neighbour, end);
neighbour.f = neighbour.g + neighbour.heuristic;
neighbour.previous = current;
}
}
}
} else {
println("no solution");
drawWindowBestFirst();
noLoop();
return;
}
drawWindowAStar();
}Pathfinding Algorithm 2 - Best First Algorithm (0:54 - 1:33 & 4:36 - 4:46)
Best-first solely use h value as factor without considering route length.
It choose the cell with closest distance towards exit and add following paths to choice stack. Repeat such process till current cell is the destination.
Compred with A*, best first is more straightforward. Yet, it’s greatest setback is that it doesn’t guarantee best path.
Although it’s not that obvious, for mazes with limted path choice, best first has the best performance. This is mainly because there’s one and only correct path to the destination.
Same as A*, it needs to know the exact position of the destinaton, or it is not applicable.
void BestFirst() {
if (route.size() > 0) {
int winner = 0;
float minDist = heuristic(route.get(winner), end);
for (int i = 0; i < route.size(); i++) {
float dist = heuristic(route.get(i), end);
if (dist < minDist) {
minDist = dist;
winner = i;
}
}
current = route.get(winner);
if (current == end) {
findPath = true;
println("Found");
drawWindowBestFirst();
return;
}
route.remove(current);
ArrayList<Cell> neighbours = current.neighbours;
for (Cell neighbour : neighbours) {
if (!neighbour.visited) {
neighbour.visited = true;
neighbour.previous = current;
route.add(neighbour);
}
}
drawWindowBestFirst();
} else {
println("no solution");
drawWindowBestFirst();
noLoop();
return;
}
}Pathfinding Algorithm 3 - Breadth First Algorithm (1:33 - 2:13 & 4:46 - 5:36)
A classic search algorithm.
It add all the sub-path to the path pool and go over them in sequence till finding the route to destination.
You can also check more details in Wikipedia.
This is a slow yet stable algorithm. Still, it has a simple logic and can definitely give you the best path - with efficiency and storage space as exchange.
Also, it doesn’t need to exit position. In overall, a stable and basic algorithm.
Pathfinding Algorithm 4 - Depth First Algorithm (2:13 - 2:42 & 5:36 - 5:47)
Another classic algorithm corresponding to BFS. DFS choose the first possible path from the list and add following sub-path to the start of the list. Then, it repeats such process till current cell is the destination
Moreover, different adding preference would greatly affect its performance. As I set preference to left and bottom, it gains relative higher performance.
DFS has great deviation in performance and is purely by luck, Also, it cannot guarantee best solution. Therefore, if you use DFS in mazes with relatively more path choice, it would ususally get outrageous results.
Same as BFS, it is a basic algorithm that doesn’t need exit info. Thus, if you need to quickly find one path without need of best solution, you can use DFS.
Pathfinding Algorithm 5 - Dijkstra Algorithm (2:42 - 3:24 & 5:47 - 6:37)
Dijkstra solely use route length to make decision. With starting point of length 0, each step add one to the route length. Dijkstra choose the path with least length and add following paths.
Meanwhile, if the original route of sub-path has greater length than current one, replace it.
However, the problem is… Since each cell’s distance is one, all routes has same length at each round of decision.
Thus, Dijkstra has no difference with Breadth First Search in this case.
Still, if there’s difference in length of path choice, Dijkstra can effectively optimize the choice of path.
void Dijkstra() {
if (route.size() > 0) {
int winner = 0;
for (int i = 0; i < route.size(); i++) {
if (route.get(i).dist < route.get(winner).dist) {
winner = i;
}
}
current = route.get(winner);
current.visited = true;
if (current == end) {
findPath = true;
println("Found");
drawWindowDijkstra();
return;
}
route.remove(current);
ArrayList<Cell> neighbours = current.neighbours;
for (Cell neighbour : neighbours) {
if (!neighbour.visited) {
int alt = current.dist + 1;
if (alt < neighbour.dist) {
neighbour.dist = alt;
neighbour.previous = current;
}
}
}
} else {
println("no solution");
noLoop();
return;
}
drawWindowDijkstra();
}Extra Thing to Mention
While A* consider h value and g value equally, by switching the weight of these two, they would reach drastically different appearance - with Best-First and Dijkstra as two extreme.
- When route length takes lead, A* turns into Dijkstra
- When length to exit takes lead, A* turns into Best-First
Therefore, we can change h function - like Pythagoras dist or tilt distance according to the actual need.
